[BOJ]2292번 벌집(Python)
https://www.acmicpc.net/problem/2292
2292번: 벌집
위의 그림과 같이 육각형으로 이루어진 벌집이 있다. 그림에서 보는 바와 같이 중앙의 방 1부터 시작해서 이웃하는 방에 돌아가면서 1씩 증가하는 번호를 주소로 매길 수 있다. 숫자 N이 주어졌
www.acmicpc.net
문제

위의 그림과 같이 육각형으로 이루어진 벌집이 있다. 그림에서 보는 바와 같이 중앙의 방 1부터 시작해서 이웃하는 방에 돌아가면서 1씩 증가하는 번호를 주소로 매길 수 있다. 숫자 N이 주어졌을 때, 벌집의 중앙 1에서 N번 방까지 최소 개수의 방을 지나서 갈 때 몇 개의 방을 지나가는지(시작과 끝을 포함하여)를 계산하는 프로그램을 작성하시오. 예를 들면, 13까지는 3개, 58까지는 5개를 지난다.
입력
첫째 줄에 N(1 ≤ N ≤ 1,000,000,000)이 주어진다.
출력
입력으로 주어진 방까지 최소 개수의 방을 지나서 갈 때 몇 개의 방을 지나는지 출력한다.
예제 입력 1
13
예제 출력 1
3해설
입력받은 숫자의 방까지 나가기 위해 몇 번의 방문을 열어야 하는지 계산하는 문제이다. 처음 이 문제를 보았을 때, 전자 최외각 전자 수, 전자 배치 이런 걸 생각했는데 상관없으니까 접고..
이 문제를 많은 사람들이 반복문으로 풀었지만 나는 좀 더 수학적으로 접근하겠다.
백준은 테스트 케이스를 굉장히 조금 주는데 이 문제는 친절하게도 그림으로 더 많은 케이스를 세어 볼 수 있다.
1번 방 => 1
2~7번방 => 2,
8~19번 방 => 3
20~37번 방 => 4
38~61번 방 => 5
끝 번만 생각 했을때,
1 7 19 37 61...로 나열되고, 증가하는 숫자의 규칙성이 있으니 고등학교 때 배운 계차 수열이 생각났다.
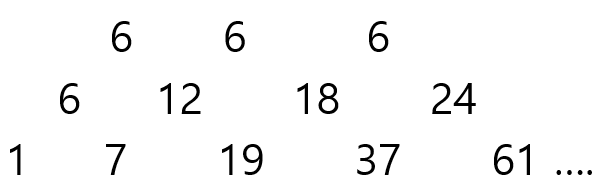
https://www.mathfactory.net/10916
계차수열의 뜻과 계차수열로 원래 수열의 일반항 구하는 방법
계차수열의 뜻 수열에서 한 항과 그 바로 앞 항의 차를 계차라고 해요. 그리고 계차들로 이루어진 수열을 계차수열이라고 합니다. 예를 들어 다음과 같은 수열이 있다고 할게요. \begin{gather*} 1, \
www.mathfactory.net
위 글을 참고해서 계차수열의 점화식을 구하면 bn = 6n이고
$$ a_{n}= 3n^{2} - 3n + 1 $$
우리는 여기서 an을 구하는 게 아니다.
문자를 잘 이해해보면 여기서 n은 몇 번째 둘레고 an은 입력받은 숫자다.
입력받은 숫자가 n번째 수열보다 작고 n-1보다 크면 그 an은 n을 출력하면 된다.
따라서 우리는 저 점화식을 n에 대해서 유도해야 한다.
공식 유도
an을 이항 시켜서
한쪽을 0으로 만들고
이 상태로 n에 대한 해를 구하기 위해 아래의 근의 공식을 적용시켜보자,
$$ x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a} $$
그러면,
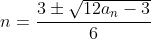
여기서 an 은 방의 번호니까 자연수이다. 그러면 최솟값은 1인데
1일 때 , n 은 0이 된다. an이 커질수록 음수가 되기 때문에,
해는
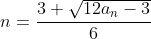
an는 input 값이고 이 식을 토대로 코드를 작성하면
print((3+(12*int(input())-3)**.5)//6)이런 식으로 식을 쓸 수 있다. 하지만 실수가 나오기 때문에 int()로 한번 형 변환시켜준다.
print(int((3+(12*int(input())-3)**.5)//6))그리고 입력을 쭉 해봤는데
1 1
2 1
.
.
.
7 2
이런 식으로 나옴
2부터는 2가 나와야 한다. 올림을 하기엔 7도 2가 나와야 하기 때문이다. 이것에 대해 엄청 고민했는데....
일단,
// 연산자는 나누기 연산 후 소수점 이하의 수를 버리고, 정수 부분의 수만 구하는 연산
>>> -9/1
-9.0
>>> -9/2
-4.5
>>> -9/3
-3.0
>>> -9/4
-2.25
>>> -9/5
-1.8
>>> -9/6
-1.5
>>> -9//1
-9
>>> -9//2
-5
>>> -9//3
-3
>>> -9//4
-3
>>> -9//5
-2
>>> 9//1
9
>>> 9//2
4
>>> 9//3
3
>>> 9//4
2
>>> 9//5
1// 연산에 대한 테스트를 해보면
양수에 대한 연산은 소수점 이하의 숫자를 버리지만
음수는 올림을 하는 것을 볼 수 있다.
이를 이용해서 코드를 다시 짜면
print(int(-(-(3+(12*int(input())-3)**.5)//6)))음수로 나눗셈을 한 뒤, 다시 양수로 바꿔주고 소수점을 제거하기 위해 int()로 형 변환해준다.

